Intervals – Advanced
As we learned in the previous lesson, intervals are used to measure the distance between two notes.
Intervals are named according to how many steps one must take in the scale to get there.
Fourths, Fifths, and Octaves are generally called Perfect because of their pure sound.
All other intervals are called Major if they line up with the Major Scale, or Minor if they are one half step smaller than the interval found in the major scale.
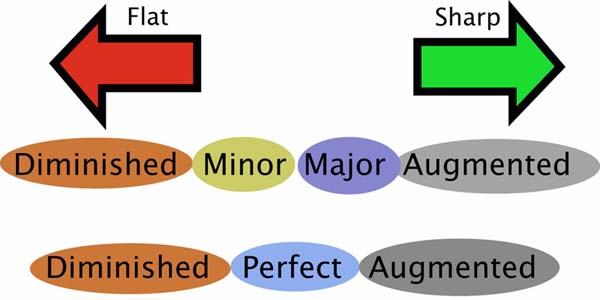
Less commonly we may see other combinations as well, such as perfect intervals being sharpened (adding a half step), or minor intervals being flattened (subtracting a half step).
Here is the general rule that describes how to name all such intervals:
Intervals which are very sharp are called “augmented”.
Intervals which are very flat are called “diminished”.
Major intervals or perfect intervals become “augmented” if a sharp is added.
Minor intervals or perfect intervals become “diminished” if a flat is added.
Half Steps
Common Name
Alternate Name
0
Unison
1
Minor 2nd
Semitone, Half Step
2
Major 2nd
3
Minor 3rd
Augmented 2nd
4
Major 3rd
5
Perfect 4th
6
Augmented 4th
Diminished 5th
7
Perfect 5th
8
Minor 6th
Augmented 5th
9
Major 6th
Diminished 7th
10
Minor 7th
Augmented 6th
11
Major 7th
12
Perfect Octave
Intervals – Advanced
Intervals – Advanced
As we learned in the previous lesson, intervals are used to measure the distance between two notes.
Intervals are named according to how many steps one must take in the scale to get there.
Fourths, Fifths, and Octaves are generally called Perfect because of their pure sound.
All other intervals are called Major if they line up with the Major Scale, or Minor if they are one half step smaller than the interval found in the major scale.
Here is the general rule that describes how to name all such intervals:
Intervals which are very sharp are called “augmented”.
Intervals which are very flat are called “diminished”.
Major intervals or perfect intervals become “augmented” if a sharp is added.
Minor intervals or perfect intervals become “diminished” if a flat is added.

| Half Steps | Common Name | Alternate Name |
| 0 | Unison | |
| 1 | Minor 2nd | Semitone, Half Step |
| 2 | Major 2nd | |
| 3 | Minor 3rd | Augmented 2nd |
| 4 | Major 3rd | |
| 5 | Perfect 4th | |
| 6 | Augmented 4th | Diminished 5th |
| 7 | Perfect 5th | |
| 8 | Minor 6th | Augmented 5th |
| 9 | Major 6th | Diminished 7th |
| 10 | Minor 7th | Augmented 6th |
| 11 | Major 7th | |
| 12 | Perfect Octave |